SharifCTF: Universal ReEncryption

This was the 100 point crypto challenge from SharifCTF dealing with a homomorphic encryption scheme based on the idea of Universal ReEncryption (URE) (hence the name of the challenge). It’s a pretty straightforward concept that made for a fun little crypto challenge that was excellently presented by the people at SharifCTF.

The Problem

For this one we are given the following prompt:

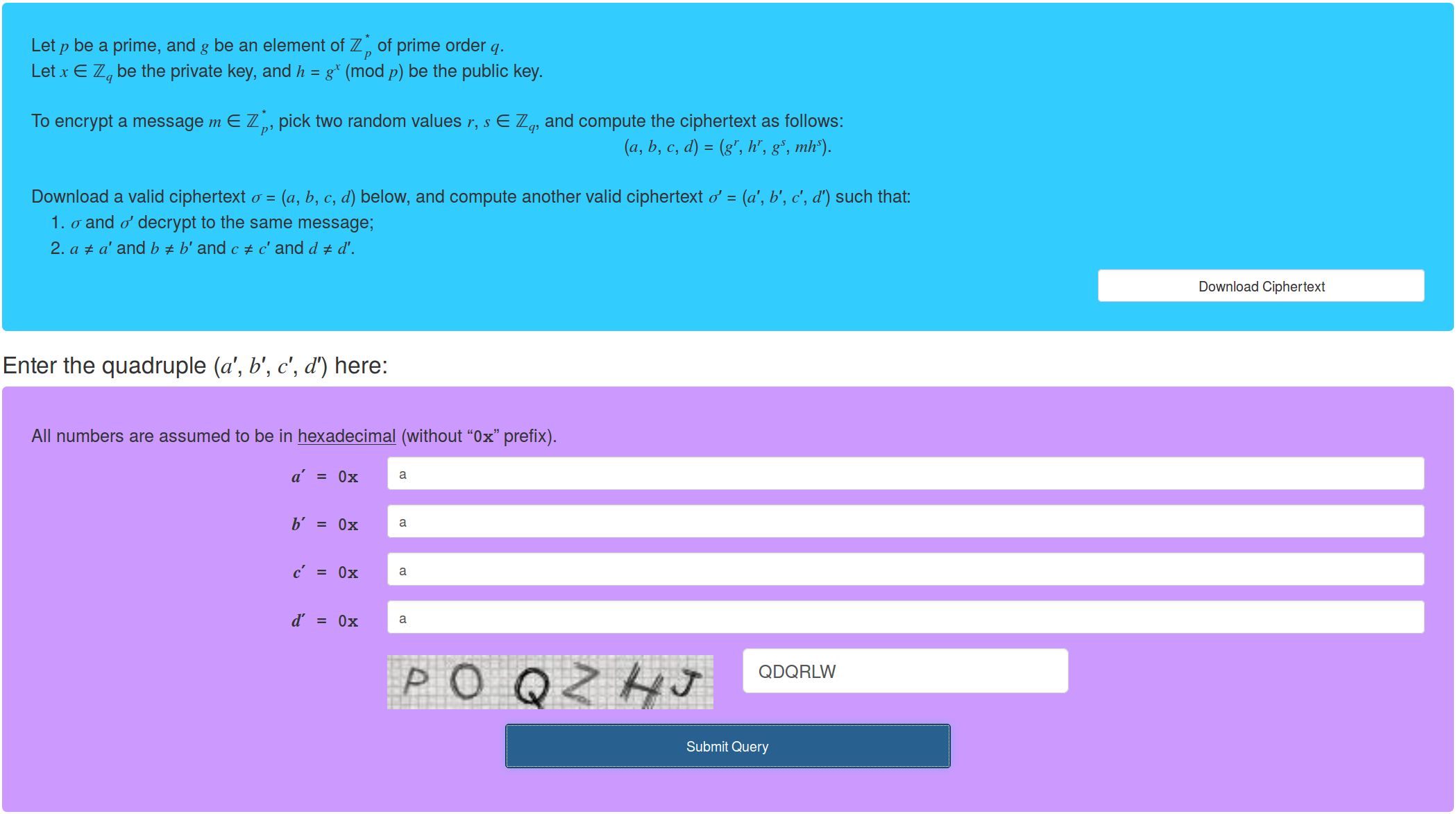
We are also given the following valid ciphertext:

Note: You require neither g nor h to solve this challenge!

p = 0x8000048d1d71b57838b7d90ebc63b8c853f3af1af87ce2db5593f3386ae5139d040d3844e31db723d39cdd7717c8cffc26f6f877b5c85ca8e595ca687c07c773

a = 0x21068b690f5438360063bb80799a95af7bbb83fa399376af9ad21e0cef3d5233aa313fe1960ccfd87e8a4b1dba0e053d89bfebd4bc57170147462fafef44c9c7
b = 0x436c161645052a76c1f7c976da63f61987f5f9bf7cb810a0e6fb1ea593aa9397c7b7cb0488f0f14cf93c79eef967a4b2a39388da1a357077d30a6f8b2a2c97e7
c = 0x7dd53b07c05ea2aca88bcbdd58601fa344918848107431ae7710542ea625abb335c27352c1bd2ef01359adb19b1bee77edc07ab0b41b9766392fc154f7891268
d = 0x1a50308011b409460d504cc7cddd61cdff1bda0774d1329b59606df274bce81a7e4b15830ddd4e684e3f2422d36bd52220134881db560be0a34c76a9c5bbb6be

The description of the challenge is pretty specific, and it is pretty clear that they just want us to understand how to apply the idea of URE in this slightly-ElGamal looking system. Using the ciphertext values given to us we just need to find another set of ciphertext messages that decrypt to the same values. Let’s just re-encrypt the ciphertext! We can’t do the described encryption method because we don’t have the public key; however, the modulus operation over $p$ occurs during the decryption phase and we have $p$! So we can’t encrypt the ciphertext, but we can find an equivalence!

We just need to find another value that solves:

The properties of modular arithmetic shows that these will be:

Checking the page source we can see that our final answers have to be $\leq128$:

<input type="text" class="form-control" id="a" maxlength="128" placeholder="Hexadecimal value for a&prime;">

Setting $n=1$ we can solve the above equations and get our new values which are $\leq128$:

$a' =$ a1068ff62cc5edae391b948f35fe4e77cfaf33153210598af06611455a2265d0ae3e7826792a86fc52272894d1d6d539b0b6e44c721f73aa2cdbfa186b4c913a

$b' =$ c36c1aa36276dfeefaafa28596c7aee1dbe9a8da7534f37c3c8f11ddfe8fa734cbc503496c0ea870ccd95766113074aeca8a8151cffdcd20b8a039f3a6345f5a

$c' =$ fdd53f94ddd05824e143a4ec14c3d86b9885376308f11489cca44767110abf5039cfab97a4dae613e6f68b28b2e4be7414b7732869e3f40f1ec58bbd7390d9db

$d' =$ 9a50350d2f25bebe460825d68a411a96530f89226d4e1576aef4612adfa1fbb782584dc7f0fb058c21dc0199eb34a51e470a40f9911e688988e2411241c37e31

Those brings up our final flag when submitted:

SharifCTF{2731b41d3dc59498b6f1ea69d2680e2b}